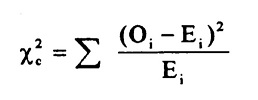/
2018.04.10 Forelesningsnotater til Glaiza
2018.04.10 Forelesningsnotater til Glaiza
MET3431, statistikk
X^2-test, chikvadrattest, uavhengighet, sammenheng
- Andeler i krysstabell
- Krav for chikvadrattest
- Tilfeldig utvalg
- Alle forventede verdier større enn 5 (E>=5 alle celler).
- O=observert frekvens
- E=Estimert\expected frekvens
- Formel:
- Chikvadrat, X^2= (
- E=(Radsum*Kolonnesum)/totalsum
Eksempeloppgave 1
- H0: Ingen sammenheng mellom kjønn og røyking.
Observed | Røyker | Røyker ikke | Total |
|---|---|---|---|
| Kvinne | 30 | 120 | 150 |
| Mann | 10 | 90 | 100 |
| Total | 40 | 210 | 250 |
- Anta at H0 er sann.
- Beregn forventede verdier ved H0=sann.
- (O-E)^2/E
- Regn ut forventede verdier dersom H0 er sann:
- E=(Radsum*Kolonnesum)/totalsum.
- E=(Antall kvinner*antall røykere)/hele populasjonen.
- E=(150*40)/250=24=Estimert antall kvinner som røyker
- E=(Antall menn*antall røykere)
- E=(100*40)/250*=16
- E=(Antall kvinner*antall røykere)/hele populasjonen.
- E=(Radsum*Kolonnesum)/totalsum.
- Regn ut forskjell mellom observert og forventet:
- (O-E)^2/E
- Chi(?) for kvinner som røyker=(kvinner som faktisk røyker-kvinner som forventes å røyke)^2/kvinner som forventes å røyke
- (30-24)^2/24=1,5
- Chi(?) for menn som røyker=(menn som faktisk røyker-menn som forventes å røyke)^2/menn som forventes å røyke
- ((10-16)^2)/16=2,25
- Osv for alle ruter.
- Chi(?) for kvinner som røyker=(kvinner som faktisk røyker-kvinner som forventes å røyke)^2/kvinner som forventes å røyke
- (O-E)^2/E
- Regn ut forventede verdier dersom H0 er sann:
- (O-E)^2/E
- Beregn testobservator ved avvik mellom ?? og forventet verdi.
- Legg sammen chi-verdiene i alle ruter.
- Testobservator=1,5+0,286+2,250+0,429=4,465
- Legg sammen chi-verdiene i alle ruter.
- Test mot en kritisk verdi fra tabell.
- Frihetsgrader=(kolonner-1)(rader-1)
- (2-1)(2-1)=1*1=1
- Kritisk verdi alfa (0,05), med 1 df i tabell = 3,84 = X^2a/chikvadratalfa.
- Testobservator er utenfor kritisk verdi, H0 forkastes. Vi kan ikke si at det ikke er sammenheng mellom kjønn og røyking.
- Frihetsgrader=(kolonner-1)(rader-1)
E, H0-verdier | Røyker | Røyker ikke | Total |
|---|---|---|---|
| Kvinne | 24 | 126 | 150 |
| Mann | 16 | 84 | 100 |
| Total | 40 | 210 | 250 |
Chi(?) | Røyker | Røyker ikke | Total |
|---|---|---|---|
| Kvinne | 1,500 | 0,286 | 1,786 |
| Mann | 2,250 | 0,429 | 2,679 |
| Total | 3,750 | 0,714 | 4,464 |
Eksempeloppgave 2
- Anta at H0 er sann.
- Beregn forventede verdier ved H0=sann.
- (O-E)^2/E
- Regn ut forventede verdier dersom H0 er sann:
- Regn ut forskjell mellom observert og forventet:
- (O-E)^2/E
- Beregn testobservator ved avvik mellom ?? og forventet verdi.
- Legg sammen chi-verdiene i alle ruter.
- Testobservator=21,437
- Legg sammen chi-verdiene i alle ruter.
- Test mot en kritisk verdi fra tabell.
- Frihetsgrader=2
- Kritisk verdi chikvadratalfa=5,991
Observert | Mor: Ungd.skole | Mor: VGS | Mor: Høy.utd. | Total |
|---|---|---|---|---|
| Stille leksested | 271 | 1477 | 3102 | 4850 |
| Ikke stille leksested | 33 | 116 | 167 | 316 |
| 304 | 1593 | 3269 | 5166 |
Expected | Mor: Ungd.skole | Mor: VGS | Mor: Høy.utd. | Total |
|---|---|---|---|---|
| Stille leksested | 285,40 | 1 495,56 | 3 069,04 | 4 850,00 |
| Ikke stille leksested | 18,60 | 97,44 | 199,96 | 316,00 |
| 304,00 | 1 593,00 | 3 269,00 | 5 166,00 |
Testobservator X^2 | Mor: Ungd.skole | Mor: VGS | Mor: Høy.utd. | Total |
|---|---|---|---|---|
| Stille leksested | 0,727 | 0,230 | 0,354 | 1,311 |
| Ikke stille leksested | 11,158 | 3,534 | 5,434 | 20,126 |
| 11,885 | 3,764 | 5,788 | 21,437 |
| Testobservator, kritisk verdi, X^2= | 21,44 |
| Frihetsgrader | 2 |
| ta, X^2a= | 5,991 |
| Chikvadrat X^2 > Chkvadratalfa X^2a, forkast H0 | |
Undertemaer:
Label:
Filter by label
There are no items with the selected labels at this time.
Relatert label A:
Filter by label
There are no items with the selected labels at this time.
Relatert label B:
Filter by label
There are no items with the selected labels at this time.
, multiple selections available,
Related content
Lvl1: Ancient Catacombs, Tomb of the Ancients
Lvl1: Ancient Catacombs, Tomb of the Ancients
More like this
Lvl 50: Underground Enclave
Lvl 50: Underground Enclave
More like this
Sands of Time (the hour glass rupture, Apexius)
Sands of Time (the hour glass rupture, Apexius)
More like this
Lvl 45: Elysia's Chamber
Lvl 45: Elysia's Chamber
More like this
Lvl 38: Grave Digger's Cove
Lvl 38: Grave Digger's Cove
More like this
test footer